How Cross Entropy Loss With Label Smoothing Works

I wrote an app to classify an object using transfer learning, and the model was trained on CIFAR-10 dataset, all by myself.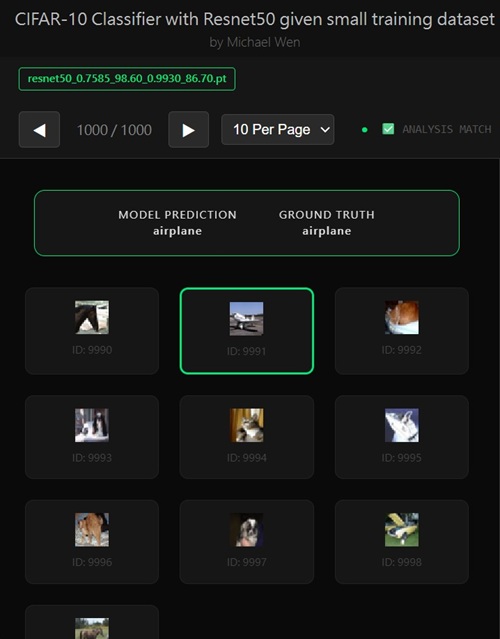

Cross-Entropy Loss with Label Smoothing

With label smoothing, the cross-entropy loss will not be zero, even when the model’s predicted probability distribution exactly matches the target distribution. This behavior is expected and intentional.

Label Smoothing Target Distribution

For a classification problem with K classes and smoothing factor ε, the target labels are defined as:

• True class: 1 − ε
• All other classes: ε / (K − 1)

As a result, the target label is no longer one-hot and instead forms a probability distribution with non-zero mass assigned to all classes.

Cross-Entropy Loss Formula

The cross-entropy loss is defined as: L = − ∑ yi log(pi) If the model predicts the exact smoothed target distribution (i.e., pi = yi for all classes), the loss becomes: Lmin = − ∑ yi log(yi) This value is the entropy of the smoothed label distribution.

Why the Loss Is Never Zero

Entropy is zero only for a perfectly certain (one-hot) distribution. Because label smoothing explicitly introduces uncertainty into the target labels, the entropy — and therefore the minimum possible loss — is always greater than zero.

Example

• Number of classes: K = 10
• Label smoothing factor: ε = 0.1

Target probabilities:

• True class: 0.9
• Each other class: 0.1 / 9 ≈ 0.0111

Even with perfect prediction, the minimum loss is approximately (assuming we use natural log, which is what torch.nn.CrossEntropyLoss uses):

Lmin = −[0.9*log0.9+9*0.0111*log0.0111] ≈ 0.544

Practical Implications

• Training loss will not converge to zero.
• Lower loss values are not directly comparable to runs without label smoothing.
• Improved generalization and calibration are expected benefits.

Key Takeaway

With label smoothing, a non-zero minimum loss is expected — even for perfect predictions — because uncertainty is deliberately built into the target distribution.

Any comments? Feel free to participate below in the Facebook comment section.